مساحة شبه المنحرف بالطرق المختلفة

منطقة شبه محدودة بطرق مختلفة تتجاوز موقع محتوىشبه المؤقت من الأشكال الأساسية للهندسة ، والتي لها طرق مختلفة للاستخدام في النظرية الهندسية والعملية والفيزيائية ، واستنادا إلى ذلك هو كيفية حساب المنطقة شبه المقسمة.

شبه المنحرف

أحد الأشكال الهندسية الرئيسية ، ويتكون من ضلوع متوازيين معاكسة على الأقل ، لأنه شكل أربعة أضعاف ، حيث يكون الجانبين فقط متوازيين بينما يعتبران بالتوازي مع الأضلاع ، وهو شكل دقيق تمامًا للشكل شبه المنحرفعندما تتضمن الأحزاب شبه المتوازية ، لكنها ليست متساوية ، وبالتالي فإن أكبر الأضلاع فيها تمثل القاعدة الكبيرة ، وأصغر قاعدة.

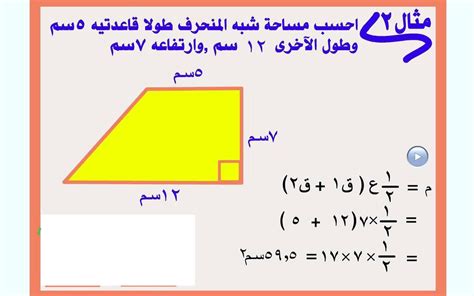
حساب مساحة شبه المنحرف

عدد مساحة شبه منحرف بأكثر من معادلة رياضية وطريقة رياضية ، بين القاعدة الأولى التي تقول إنها مساحة شبه المنحرف = (طول القاعدة الرئيسية + الحد الأدنى للطول الأساسي) \ 2) x الارتفاع.

أي أن المنطقة شبه المؤقتة = (مجموع القاعدتين \ 2) x الارتفاع ، تجدر الإشارة إلى أن الارتفاع في زاوية نصف الظهور هو جانب واحد من الأضلاع شبه المقسمة في القاعدة الرئيسية ، ولكن في الأنواع الأخرى شبه المحببة هي المسافة الرأسية بين القاعدين المتوازيين.

أما بالنسبة للطريقة الثانية للحساب مساحة شبه Deviant يفصل شبه المنحرف في الأشكال مثل المستطيل أو المثلث أو المربع أو المثلث أو الأضلاع المتوازية ، والمثلث ، بغض النظر عن الأشكال الهندسية.

ولكن ما هو المقصود هو أن فصل النموذج الهندسي سهل حساب مساحته ، ثم حساب كل شكل هندسي ، مثل نصف مقسوم إلى ثلاثة أشكال من المثلثات والمستطيلات ، بحيث تكون المنطقة نصف المقسّمة ، وهي منطقة ثلاثية أول + منطقة مثلث ثانية.

انواع شبه المنحرف

أولاً ، منحرف عام ، وهو شبه المنحرف إنه مضلع رباعي الأضلاع ، وهناك ضلوعان متوازيان ولديه نقطتان غير متساوتين يلتقيان عند نقطة واحدة ، ومن هنا ، يكون الارتفاع هو المسافة الرأسية بين الجانبين المتوازيين ، وبالتالي فإن هذا النوع شبه المدعوم يتكون من أربعة زوايا غير متساوية من 360 درجة ، وتوصيلان بين المساعرين يساوي 180 درجة.
ثانياً ، قدمًا متساوية تقريبًا ، حيث يوجد جانبان متوازيان معاكسًا ، والجانبين الآخرين معاكسان ، متساويان في الطول ، وليس متوازيًا ، ويساوي طول القطر.
ثالثًا ، ضلع شبه مفصل ومختلف ، ويتألف من أربعة أضلاع ، واثنين من المتوازيين ، غير متكافئين ، ويمثلون القاعدة شبه المستمر ، واثنان ليسا أوجهاً مما يوجه ويساويان ولديهما نقطتان غير متكافئين يعبران عند نقطة واحدة.
تمثل الزاوية الرابعة الموجودة ، شبه المتوحنة ، حيث تشمل زاويتين حاليتين ، ويمثل ارتفاع هذا النوع من النصف ، الضلع العمودي في القاعدة الرئيسية ، والتي هي بالطبع واحدة من أهم الأضلاع المنحرفة وتمثل الارتفاع شبه المؤقت.

قدمنا لك من خلال موقع محتوى أكثر مساحة شبه هُزمت ، مع طرق رياضية مختلفة ، بالإضافة إلى توضيح أهم أنواع الأشكال شبه الموسعة في الرياضيات والهندسة.