يعد الكسر أحد أنواع النسب التي تعبر عن العلاقات النسبية بين جزء من العنصر مع الجميع ، بحيث يرتبط كلا الرقمين بعلاقة الجزء ككل ، وسنتعرف على الأنواع التالية من الكسور.
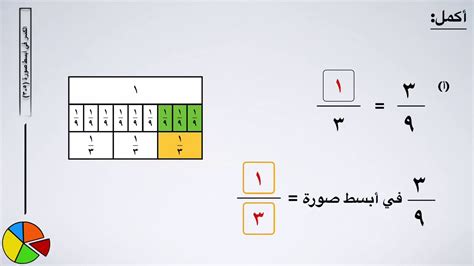
الكسور التي في أبسط صورة
الكسور ذلك في أبسط Image “src =” https://www.m7utwa.com/wp-connet التي في أبسط صورة “width =” 600 “height =” 361 “srcset =” https://www.m7utwa.com/wp-connet https://www.m7utwa.com/wp-contrent https://www.m7utwa.com/wp-contrent https:
إذا واجهت مشكلة رياضية ، فيجب عليك اختيار الكسور التي يجب أن تركز بشكل جيد على حقيقة أن الكسور لا تقبل الانفصال بأي رقم أبسط من الحالة.
مثال 1: (12/16 ، 5/3 ، 25/5) يستريح في أبسط صورة هنا هي 5/3 ، حيث لا يمكن تبسيطها أكثر مما هي عليه.
مثال 2: (4/3 ، ¼ ، 14/7) إذا كانت هذه هي الانتخابات المتاحة ، فيجب أن تكون متوفرة لأكثر من إجابة واحدة ، حيث تأتي كلا الكسور 4/3 و 1/4 في أبسط شكل.
لا تفوتك أيضًا: كل كسر أدناه لا يساوي كسور أخرى
أنواع الكسور الرياضية
من الممكن التعبير الكسور التي في أبسط صورة مكونة ، يتم التعبير عنها أنواع الكسورأو طرق محتملة لكتابتها.
1- الكسر الاعتيادي
إنها استراحة مفصولة بأرقامها من خلال حالة العلامة التجارية (/) أو (__) شريطة أن يكون أحد البسط والآخر هو المكان ، ونكتشف أن هذا النوع من الفروع في ثلاثة أنواع:
- جزء: في هذا النوع ، يكون الرقم الذي يعبر عن البسط أصغر من الرقم الذي يعبر عنه Maqam ، مثل: 2/3 ، 5/6 ، 3/9 ، 4/7 ، إلخ.
- كسريُعرف باسم الكسر غير المعتاد ، وهي قيمة عدد البسط أو أكبر من قيمة رقم Maqam أو تساويها ، مثل: 5/5 ، 8/2 ، 9/7 ، إلخ.
- كسر: يُعرف باسم عدد الكسر ، الذي يتكون من عدد حقيقي وكسر بسيط ، مثل: 2 4/5 ، 5 6/9 ، إلخ.
2- الكسر العشري
يتم التعبير عنه باستخدام الفاصلة العشرية ، شريطة أن تأتي الأرقام إلى الجانب الأيمن من الفاصلة ، إذا كان الكسر مكتوبًا باللغة الإنجليزية ، مثل: 0.5 ، 0.987 ، أو اللغة العربية مثل 0.225 ، 0.88 ، 0.4
أنواع العمليات التي تُجرى على الكسور
من الضروري أن تكون على دراية تامة بجميع أنواع العمليات التي يتم تنفيذها في الكسور من أجل توفير الكثير من الوقت لحلها من أجل تسهيل الأمر ، مع العلم أن أنواع العمليات مقسمة إلى نوعين.
أولًا: العمليات الحسابية
النوع الأول من العمليات التي يتم إجراؤها في الكسور والأكثر شيوعًا هي الحسابات ، والتي تشمل الجمع والخصومات والضرب والأقسام.
1- الجمع والطرح
إذا كان للسجاد والوضع في الكسر أو التكوين الطبيعي نفس القيمة ، فإن الجمع والطرح هما الحسابات التي يتم تنفيذها كمراحل الأخيرة من كلا الكسور.
من أجل القيام بذلك عن طريق جمع البسط إلى البسط ، أو عن طريق وضعه من بعضهم البعض ، مع مراعاة المكان الذي يحتفظ به لأنه موحد ، على سبيل المثال: 3/5 + 6/5 = 9/5
إذا كانت الأضرحة مختلفة في كسرين ، فمن الضروري إجراء عملية الانضمام إلى الأضرحة أولاً قبل تقديم العرض أو المجموعة.
شريطة أن يتم ذلك من خلال العثور على أدنى مضاعف لاتحاد سكان اثنين ، على سبيل المثال: 2/3 +1/2 والمضاعف المشترك هنا هو الرقم 6 ، وبالتالي فإن المهمة هي الآن لتوحيد الأضرحة لتصبح 6
يتم ذلك عن طريق ضرب الكسر الأول في الرقم 2 والكسر الثاني في 3 ، ليصبح النموذج التالي: 4/6 + 3/6 الآن بعد توحيد الأضرحة.
ولكن إذا كانت الأرقام عبارة عن كسور مختلطة ، فليس من الممكن أداء الجمع أو تقديمه ، ما لم يتم تحويله إلى كسر في مجمع (كسر غير عادي).
إذا تم توحيد الأضرحة بعد التحويل ، فهي متاحة لأداء مجموعة الجمع أو الطرح في عدد البسط بينما يخزن أرقام البلد كما هي.
ولكن إذا لم يكن الأمر متشابهًا ، فستتبع الطريقة السابقة النتيجة المزدوجة الأصغر للانضمام إليهم أولاً ، ثم تنفيذ التجمعات أو من خلال تقديمها بنفس الطريقة.
مثال: 1 2/6 + 2 ¼ هنا ننتقل كسور مختلطة إلى مركبة لتصبح كلا الرقمين في الجسم 8/6 + 9/4
(يتم ذلك عن طريق ضرب الرقم الصحيح في مكانه ، ثم إضافة قيمة البسط إلى المنتج ، أي 1 × 6 = 6 ، ثم 6+2 = 8 ، لذلك أصبحت قيمة البسط 8 بينما يبقى البسط كما هو)
ثم نجمع بين الأضرحة عن طريق التغلب على أزواج مشتركة ، والتي هي 24 ، لذلك نضاعف الكسر الأول في الرقم 4 والكسر الثاني في الرقم 6 ليصبح الكسور في الجسم 32/24 + 54/24 = 86/24
للعثور على أبسط شكل من أشكال الكسر ، نقسم العامل المشترك النهائي ، وهو الرقم 2 ، وبالتالي تصبح النتيجة 43/12
تجدر الإشارة إلى أن أداء إمدادات الكسر بجميع الأنواع يتطلب نفس الخطوات المتخذة في العمليات التعددية ، لذلك من المهم معرفة تمامًا خصائص العرض التقليدي.
2- الضرب والقسمة
من السهل إجراء عملية الضرب في كسور بسيطة ، حيث يتم ذلك عن طريق ضرب الرقم في البسط في عدد الأرقام المماثلة ، والرقم في البلد في البلاد المعني.
مثال: 2/3 * 7/4 والنتيجة هي 14/12 ، ولكن إذا كان الكسر مختلطًا ، فمن الضروري تحويله إلى فترات مركب أولاً ، ثم تنفيذ عملية الضرب بنفس الطريقة التي كان من قبل.
مثال: 1 2/3 * 2 ¾ يتم النقل بالطريقة المذكورة سابقًا (في الكسر الأول ، يتم التغلب على الرقم 1 * 3 ، ثم يتم إضافة الرقم 2 إلى الإخراج ، والمكان كما هو ، لذلك يصبح الكسر 5/3 ، والمسألة هي أيضًا في الاستراحة الثانية)
المسألة موجودة في الجسم 5/3 * 11/5 = 55/15 من هنا ، يمكن تنفيذ إيقاع أو فصل ، لأن توحيد الأضرحة غير مطلوب.
تجدر الإشارة إلى أن الفصل مع الكسور يتطلب تحويل علامة الانقسام إلى إيقاع ، ثم قلب الضريح وإنشاء الكسر الثاني ، ثم عملية الضرب العادية والنتيجة هي نتيجة الفصل.
مثال: 2/3 مقسومًا على 5/7 ، من أجل العثور على إنتاج الإنتاج. يجب أن تكون المسألة في الجسم: 2/3 * 7/5 بحيث تكون النتيجة 14/15 ببساطة.
وبالمثل ، إذا كانت الكسور من النوع المختلط ، فسنحولها أولاً إلى كسور مركبة ، ثم اتخذ الخطوة السابقة حول إصدار الانفصال ، للعودة إلى مسألة الضرب.
مثال: 1 ¾ مقسمة إلى 2 ¼ تحولت إلى كسور معقدة ، لذلك يتم على الجسم 7/4 مقسومًا على 9/4 ، ثم اتبع خطوة النقل إلى إيقاع ، لتصبح الرقم 7/4 * 4/9 = 28/36
يمكن أن تكون الكسور في أبسط صورة من خلال مشاركة العامل المشترك إلى الحد الأقصى ، وهو 2 لتصبح نتيجة الكسر النهائي في أبسط صورة هي 14/15
لا تفوتك أيضًا: الكسر الآخر أقرب إلى أقرب النصف
ثانيًا: العمليات المنطقية
العمليات المنطقية هي العمليات التي أجريت في كسور من أنواع مختلفة لغرض مقارنتها ، والمعرفة إذا كانت العلاقة بينهما أكبر أو أصغر أو تساوي بعضها.
حيث الرمز (<) i referohet marrëdhënies së më të madhit, ndërsa simboli (>) يشير إلى أصغر علاقة ، في حين أن الرمز (=) هو قصة علاقة المساواة كما هو معروف.
1- كسور ذات مقامات مُوحدة
في هذا النوع من الكسر ، يمكن مقارنته بسهولة ، حيث يعبر كل كسر عن قيمة رقمه ، وبالتالي فإن أكبر كسر هو أكبر كسر في قيمته.
| كسر | علاقته مع الآخر |
| ¾ | كبير |
| 2/4 | الأصغر |
2- كسور ذات بسط مُوحد
إذا كانت الكسور المقارنة بينهما هي قيم التبسيط مساوية لبعضها البعض ، فإن أكبر كسر هو أصغر كسر.
| كسر | علاقته مع الآخر |
| 4/8 | الأصغر |
| 4/5 | كبير |
3- كسور مختلفة المقامات والبسط
في سياق الحديث عن الكسور التي في أبسط صورة إذا كان كل من السجاد والموقف مختلفًا ، فإن المقارنة بين الكسرين تتطلب منك أولاً اتباع بعض الخطوات لتوحيد الأضرحة بحيث يمكنك مقارنتها.
- توحيد الأضرحة في كسرين.
- العثور على أصغر مضاعف مشترك بينهما.
- وضع الكسر الذي يحتاج إلى توحيد ليصبح ككسر ثاني في أبسط أشكال في المضاعف المعتاد لتوحيد الأضرحة.
- مقارنة الكسور بعد أن يكون لها مزارات مماثلة.
مثال: إذا كان كلا الكسوران 5/3 و 4/6 ، فإن مضاعفة أصغر الشائع بينهما هو الرقم 2 ، لذلك وصلنا إلى أن يكون الباقي الأول فيه في شكل 10/6
وبالتالي ، نلاحظ أن المحطات في كلا الكسور أصبحت متشابهة ، لذلك كلا الكسور هي 10/6 و 4/6 الآن نتبع العملية المنطقية في الكسر مع محطات موحدة للمقارنة ، ونجد أن العلاقة أدناه: 10/6 <4/6
لا تفوتك أيضًا: كيفية ضبط الكسور من أصغر إلى أكبر
حتى تتمكن من العثور على النتيجة الصحيحة بسهولة ، وتقليمها ووضعها أمامك في شكل نقاط متتالية حتى تتمكن من جمعها في عقلك وتذكرها جيدًا.
- يتم جمع الكسور الموحدة عن طريق جمع كل من nibblists معًا ، والحفاظ على المكان الموحد كما هو (5/8 + 6/8 = 11/8).
- يتطلب إطلاق shrracts الموحدة اقتراح اثنين من nibblicals من بعضهما البعض ، والحفاظ على الموضع الموحد كما هو (7/5 – 3/5 = 4/5)
- تحتاج إلى البحث عن مضاعف عادي وتحويل الكسر إلى أبسط صورة لإنهاء الجمع أو من خلال توفير العمليات في الكسور بأماكن مختلفة.
- لا تتطلب الكسور الضرب اتحاد الأضرحة ، ولكن يجب أن يتم ضرب كل رقم في ما يتم تحقيقه من خلال الكسر الآخر في نفس المكان (أي السجاد* البسط والمكان* …





اترك تعليقاً