تعتبر المثلثات المماثلة رياضات مشهورة ، نظرًا للتطبيقات المختلفة والنماذج الهندسية القائمة عليها بسبب أهميتها ، سواء في بناء المنازل أو النماذج المعمارية المختلفة.
مقدمة عن المثلثات المتشابهة
- المثلثات الأكثر أهمية أشكال الهندسة والأكثر شهرة يرجع إلى هيكله الهندسي ، حيث يعتبر المثلث أحد الأشكال الهندسية الثلاثية وبالتالي فهو أحد أقوى الأشكال الهندسية.
- لذلك يستخدمه المهندسون في أعمال البناء المختلفة ، بسبب قدرته على تحمل الظروف والأوزان مختلف أن الأضلاع المختلفة للمثلثات تتميز بربطها معًا وهذا الرابطة يعطي المثلثات القوة اللازمة.
- لذلك ، فلا عجب أن نجد الاهتمام الكبير بالمثلثات من علماء الرياضيات وعلماء الهندسة.
- حيث ينشئ هؤلاء العلماء قوانين خاصة لدراسة المثلثات ، وكانت هذه القوانين معروفة باسم القوانين حساب المثلث.
- تم تعيينه القوانين والنظرية مختلفة للتعرف على العلاقة بين أضلاع المثلث.
- وكذلك للدراسة زوايا وتحديد أنواع المثلث ثم تعرف على علاقات مثلثات مختلفة مع بعضها البعض.
- تم استخدام هذا في هندسة وحياة مختلفة.
- من بين أهم القوانين التي يتم إنشاؤها القوانين التي تحدد علاقة ثلاثية مع مثلث آخر من حيث الكونغرس أو التشابه.
- في هذه المقالة سنقدم كيفية معرفتها المثلثات المتشابهةوأي التطبيقات التي يمكن أن نستفيد من تشابه المثلثات.
انظر أيضا: أنواع المثلثات بواسطة الأضلاع حسب الزوايا
تعريف المثلثات المتشابهة
- لتحقيق التعريف الصحيح ، يجب أن يُعرف تشابه المثلثات بأنه يعرف المثلث وأنواعه.
- يعتبر المثلث أحد الأشكال الأساسية للهندسة في الرياضيات ، وهو ثلاثة جوانب صحيحة. تتقارب كل جانبان إلى نقطة واحدة ، وبالتالي فإن النقطة بين كل من الجانبين تسمى زاوية ، والتي تكون إما حادة أو واقعة أو منفصلة ، ويحتوي المثلث أيضًا على ثلاث زوايا.
- والمثلث بسبب تكوينه المغلق ، الذي يحتوي على ثلاثة من الاحتكاك والركن يعتبر اثنين الأبعاد.
- أحد الشروط اللازمة للمثلث الطول الكلي للضلوعين في المثلث أكثر من فريقه الأخير.
- هناك العديد من القوانين التي تتعامل مع دراسة المثلثات لتحديد مساحة المحيط والمثلثنظريات فيثاغورات.
- يعد المصطلح نظريات مماثلة أحد العلاقات الرياضية التي تشير إلى العلاقة بين المثلثات وبعضها البعض.
- وهكذا ، هذه العلاقة نسبي يخضع لشروط معينة وحالات مختلفة ، وبالتالي تستند هذه العلاقة إلى نسبة.
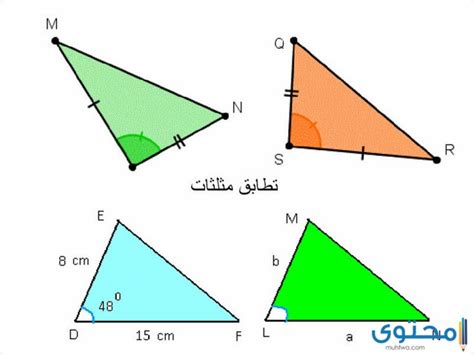
- التشابه لا يعني التطابق وفهم أنه بالنسبة لك المثال التالي ، مثلثات التالية متشابهة: مثلث أ مع نظيره ب.
- عندما اكتشف أن جميع أضلاع المثلث هي نفس قياس زوايا المثلث B ، ولكن طول أضلاع المثلث يختلف عن طول المقطوعة RIFS B بمعدل يساوي النسبة بين كل الجوانب المعاكسة. فيما يتعلق بالمطابقة ، إنها حالة توضح المثلثات مساوية لكل شيء ، من طول الأضلاع إلى الزوايا.
أنواع المثلثات
لاكتشاف المواقف التي تتشابه فيها المثلثات ، من الضروري معرفة الأنواع المختلفة من المثلثات من حيث دراسة الزوايا والأضلاع ، وبالتالي فإن أنواع المثلثات ، كما يلي بطول الأضلاع:
- مثلث متساو وفي الأضلاع الثلاثة الموجودة في المثلث متساوية في الطول ، وبالتالي فإن جميع قياسات الزاوية في المثلث متساوية ، لذلك كل زاوية في المثلث تساوي 60 درجة ، لأن مجموع زوايا المثلث يساوي 180 درجة.
- مثلث متساو أنه يحتوي فقط على طول الجانبين في المثلث متشابهان في الطول ، وكلاهما يتوافق مع الخطايا المتساوية متساوية.
- مثلث إنه مثلث لا يساوي طول أضلاعه ، وقياسات زواياها ليست متساوية. يختلف الجانب الجانبي عن طول الجانب الآخر وكل زاوية لها قياس مختلف.
انظر أيضا: تعرف على محيط المربع ومنطقتها
أنواع المثلثات حسب قياسات الزوايا
- جوارب طويلةيبلغ قياس كل زاوية أقل من 90 درجة ، ولكن في النهاية يساوي مجموع جميع الزوايا 180 درجة.
- الزاوية صحيحة: هو مثلث يحتوي على زاوية قياسه يساوي 90 درجة ، ويساوي مجموع الزاويتين الأخيرتين معًا 90 درجة.
- مثلثإنه مثلث مع زاوية تقيس أكثر من 90 درجة.
مع الإشارة إلى أنه في أي مثلث ، بغض النظر عن نوعه ، يجب أن زوايا متساوية مجموعة في حوالي 180 درجة ، وفي حالة رسم خط مستقيم مع كل جانب ، فإن الزاوية الخارجية للمثلث متساوية إجمالي زاويتين في الداخل بالنسبة للمثلث ، يتم تشغيل الزاوية التي تعلق على الزاوية الخارجية ، أو يمكن استنتاج أن الزاوية الخارجية للمثلث تساوي 180 درجة ، والتي يتم قياس الزاوية المجاورة للجلد الخارجي.
مثلثات مماثلة “src =” https://www.m7utwa.com/wp-content srcset = “https://www.m7utwa.com/wp-connet 300w
حالات تشابه المثلثات
في سياق الحديث عن المثلثات المتشابهة هناك العديد من الحالات التي نعرف من خلالها تشابه المثلثات وبعضها البعض ، وهذه هي الحالات التالية:
الحالة الأولى
- وفيه يشبه الجميع مثلث من حيث الطول ، فإنه يتناسب نسبيًا بمعنى أن كل جانبين يتوافقون مع الطول.
- دعونا نفهم هذا بطريقة أعمق ، وإذا افترضنا أن لدينا مثلثتين ، أولهما هو A ، B ، C ، والآخر هو أضلاعه ، وهما ، P. كل الأضلاع وجدت في المثلث.
العدد الثاني
- تتشابه المثلثات عندما تتشابه زاويتان في كلتا المثلثات ، على سبيل المثال ، مثلثات ABC ، والمثلث زوايا الركن ب مع زاوية P في المثلث الآخر ، كلاهما معاكس ، وكل زاوية C تساوي نظيرها ، الزاوية P في المثلث الآخر.
العدد الثالث والأخير
- حيث تتشابه المثلثات إذا كانت متشابهة جانبين وزاوية إذا كان هناك ضلوعان معاكسان في كل من المثلثتين ، وفي كلتا المثلثتين هناك زاوية تساوي كليهما ، تصبح كلا المثلثين متشابهان شريطة أن الزاوية المتساوية هي الزاوية الموجودة بين الجانبين المماثلين.
- على سبيل المثال ، لدينا مثلث ABC و Triangle ركن QP ص.
انظر أيضا: كم يتم ترك 1444 في وقت مدخل المربع
النتائج المترتبة على تشابه المثلثات
- من خلال إكمال خطابنا المثلثات المتشابهة هناك العديد من النتائج التي يمكن استخدامها اعتمادًا على الرياضية الذي ينبع من تشابه المثلثات معا.
- حيث يستخدم العلماء تشابه المثلثات في كثير التطبيقات العملية بالإضافة إلى نماذج مختلفة في البناء والهندسة المعمارية والعديد من نماذج الديكور.
- من خلال تشابه المثلثات ، نجد أن النسبة المئوية بين محيط المثلثين تساوي النسبة بين كل جانبين متعارضين في المثلثتين اللتين حدثتين بينهما.
- بنفس الطريقة نسبة اثنين من المثلثات مماثل يشبه النسبة بين طول كل جانب معاكس.
الاستخدامات العلمية لتشابه المثلثات
- قوانين ثلاثية ، بما في ذلك القوانين التي توضح تشابه المثلثات ، والاستخدام المهندسون والمصممون.
- بالإضافة إلى التعرف على قياسات الزاوية وتحديد المساحات والمحيطات للمثلثات.
- يستخدم أيضا في القضايا الجنائية فيما يتعلق بالجرائم لتوضيح تحديد انخفاض الجسم ووضع زوايا الرماية ، حيث يتم استخدامه في الغواصة البحرية.






اترك تعليقاً