وجه الاختلاف بين المربع والمعين والفرق بينهم

تحتوي المواد الهندسية على العديد من المفاهيم والأشكال المختلفة ، وأهمها أربعة أضعاف النماذج (مربع ، مستطيل ، اسمه ، أضلاع متوازية) وكان يطلق عليه هذا الاسم لأنه يتكون من أربعة جوانب ، وبالتالي يتكون من أربع زوايا ، وعلى الرغم من أنها أشكال أربع مرات ، فإنها تختلف في بعض الميزات التي تميز كل شكل عن الآخر.

وجه الاختلاف بين المربع والمعين

امزج العديد من الطلاب بين المربع والشخص الذي تم تسميته ، بالنظر إلى أن شكل كل واحد منهم قريب من حيث الطول والشكل والأيضًا خصائص.

على الرغم من المرشحين ومربع عائلة الرباعية ، فإنهم يختلفون عن بعضهم البعض في التعريف وزوايا القياس ، وما إلى ذلك ، لذلك دعونا نلقي نظرة على وجه الاختلاف وسط المربع والمعين.

تعريف المعين

تعيين واحدة من الأشكال الهندسية الرباعية.
يمكن تعريفه على أنه ضلع أربعة أضعاف ، وجميع أضلاعه متطابقة.
وكلا الجانبين. غير مهموهذا هو ، مقابل التوازي المحدد.
كل زاوية من الزوايا متساوية في القياس.

انظر أيضا: ما هو الفرق بين المربع والترشيح والمستطيل؟

جميع جوانب المسماة متساوية.
كل اثنين من الجانبين المقابلين من الأضلاع متوازية.
كل زاوية متساوية.
قطنه عمودي ، وبعضها البعض على حق ، وهم أيضًا مناسب لكل منهم.
أنه يحتوي على اثنين من زوايا حادة وزاويتين منفصلتين.
إذا كانت الزاوية تقف ، فإنها تصبح مربعًا وليست محددة.
القطن هو الوصول التناظري ، ونقطة التقاطع هي نقطة التماثل.
يعتبر شكل مستطيل لأن كل من أضلاعه يعتبر لمسة من دائرة واحدة فقط.

مجموع زوايا المعين

مجموع الزوايا المسمى 350 درجة ، ويحتوي على أربع زوايا.
كل اثنين من الزوايا المعاكسة متساوية.
أنه يحتوي على زاويتين منفصلتين وحادتين ، أي زواياها ليست متساوية في القياسات.
وإذا كانت الزوايا مساوية للقياس ، يصبح الشكل أربعة أضعاف “مربعًا”.

انظر أيضا: تعرف على محيط المربع ومنطقتها

مساحة المعين

مسافات فارغة داخل حدود أضلاعها الأربعة.
يمكن حساب المساحة من خلال ثلاث طرق ، وهي:

دلالة الارتفاع وطول أحد الأضلاع

مساحة التفاصيل = طول الضلع x.
هذا يعني ، (M = X P) ، مما يعني أن الرمز (M) يعني مساحة الاسم.
الرمز (L) يعني طول أي من الأضلاع المتساوية ، والرمز (P) هو الارتفاع.
الارتفاع (P) هو القطع المستقيم الذي يربط الجوانب المعاكسة بالتحديد.

حساب المساحة بدلالة طول القطرين

يمكن حساب مساحة الاسم من خلال طول قطر باستخدام القانون التالي:

حساب المنطقة المحددة = (القطر الأول x القطر الثاني) ÷ 2.
باستخدام الرموز M = SX ÷ 2

حساب المساحة بدلالة طول الضلع

يمكننا أن نجد مساحة المرشحين إذا كان لدينا طول أحد جانبي المرشحين ، وكذلك قياس إحدى زواياه المعروفة ، من خلال القانون أدناه:

مساحة الاسم = مربع طول أحد أنواع الجيب المحدد x أحد زواياه.
يتم التعبير عنه في الرموز: m = (l) ² x (α).

تعريف المربع

واحدة من الأشكال الهندسية الرباعية.
يمكن تعريفه على أنه ضلع رباعي على شكل رباعي ، أو شكل تربيعي ، فإن جميع أضلاعه متساوية في الطول.
وكل جانب من المربع عمودي على الآخر ، لتشكيل زاوية موجودة.
جميع الزوايا متساوية ، وكل ركن من أركان المربع 90 درجة.

انظر أيضا: أنواع المثلثات بواسطة الأضلاع حسب الزوايا

قوانين المربع

هناك سلسلة من القوانين المربعة التي يمكن من خلالها معروفة المساحة والمناطق المحيطة ، ويمكن تلخيص هذه القوانين أدناه:

القانون الأول

ينص القانون الأول على أنه يمكن حساب المنطقة المربعة من خلال منطقة المستطيل.
خاصة وأن منطقة المستطيل لها خصائص تتطابق مع المربع.
وهذا هو ، مساحة المربع = طول x ، أي. طول الأضلاع x نفسها.

القانون الثاني

تعتمد مساحة المربع على معرفة القطر.
= (مربع طول القطر /2) ، ويمكن العثور على المساحة عن طريق حساب طول القطر.

القانون الثالث

حساب المنطقة المربعة عن طريق حساب أضلاعها الأربعة.
أو ما يعرف باسم المربع المربع ، حيث يساوي محيط المربع (طول أول + ثالث + ثالث + الرابع).
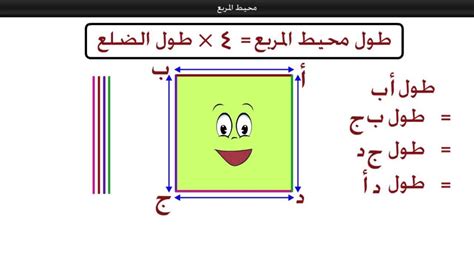
أو في صيغة أخرى أن محيط المربع = طول الأضلاع × 4.

القانون الرابع

يعتمد القانون الرابع على حساب المنطقة المربعة لحساب مربع القطري.
من خلال العديد من العمليات الرياضية المختلفة.

خصائص المربع

في سياق الحديث عن المربع والمعينيعد المربع أحد الأشكال الهندسية الأربعة التي تتميز بأشكال أخرى ومتواضعة مع العديد من الميزات ، على النحو التالي:

يتكون المربع من أربعة أضلاع وأربعة رؤوس وأربعة أحرف وأيضًا أربع زوايا داخلية.
كل ركن من زوايا القياس 90 درجة ، والقياسات الكلية لزواياها هي 360 درجة.
جميع الأضلاع متساوية في الطول.
أيضا واحد من أنواع الأضلاع المتوازية ، لأن كل من الجانبين المقابلين متوازي ومتساوي في الطول.
بالإضافة إلى ذلك ، كل زوايا زاوية متساوية في القياس.
يحتوي المربع على نقطتين فقط ، كل منهما عمودي على الآخر ، والآخر مناسب لجزأين متساويين.
الأهداف مناسبة للزوايا في زاوية متساوية في القياس ، وقياس كل واحد منها 45 درجة.
ويشمل أربعة محاور ، تسمى محاور التماثل ، اثنان منها السقوط المربع.
الاثنان الآخران هما الجزءان المستقيمين بين منتصف كل من الجانبين المقابلين للمربع ، ولا يصنعان بعضهما البعض.
نقطة الانتقال إلى المربع هي نقطة التماثل.
واحدة من خصائصها هي أيضًا أنه يميزها عن أشكال أخرى أربعة أضعاف مسطحة ، لذلك لها أبعاد مزدوجة.

انظر أيضا: كم تكلفة منطقة قطر بكيلومتر مربع

مساحة المربع

المربع هو واحد من الأشكال المهمة والفريدة الأربع الفريدة ، وخاصة في مفهوم الأشكال الهندسية بشكل عام.
لأنه يعتمد على تعريف المساحة لجميع الأشكال والوحدات المربعة.
يمكن الاعتراف بالمساحة المربعة من خلال القاعدة التالية:
منطقة مربعة = طول الضلع طول الضلع.
أو طول الأضلاع × نفسها.
أو يمكن القول أنه تم شراء الأضلاع.
مثال: طبق مربع ، طول أضلاعه يساوي 4 سم ، يجد مساحة البلاط.
مساحة الطلاء = 4 × 4 = 16 سم مربع.

محيط المربع

يمكن التعرف على محيط المربع من خلال جمع العدد الإجمالي للأضلاع ، بدءًا من الجانب الأول في الضلع الرابع.
يمكن القول أيضًا أن محيط المربع يساوي إجمالي الأطوال لأضلاعه.
أو محيط المربع = طول الأضلاع x نفسها.
مثال: لوحة الجلد ، جانبها يبلغ طوله 50 سم ، تجد محيط اللوحة؟
محيط الطلاء = 4 × 50 = 200 سم.

عدد أقطار المربع

يمكن التعرف على عدد أقطار كل شكل ضلع أو هندسي من خلال قانون خاص يشير إلى عدد أقطار كل ضلع.
حيث يتم تشكيل المضلع ، سواء كان ثلاثة أضعاف أو أربعة أضعاف أو خمس سنوات أو غيرها من الجوانب.
قانون أقطار النموذج = N (N-3) /2 ، حيث يمثل الرمز (N) عدد أضلاع المضلع.
قطر مربع = N (N-3) / 2 = 4 X (4-3) / /2
يسمح عدد أقطار المربع هو نقطتان فقط.

بمجرد أن نعرف وجه الاختلاف بين المربع الشخص الذي وجد بعض التغييرات ، بما في ذلك الخصائص والمساحة والمحيط ، ونأمل أن نكون قد تمكنا من شرح كل التفاصيل بينهما ، ويسعدنا الحصول على أي أسئلة حول قوانين الرياضيات المختلفة.