قانون مساحة الدائرة

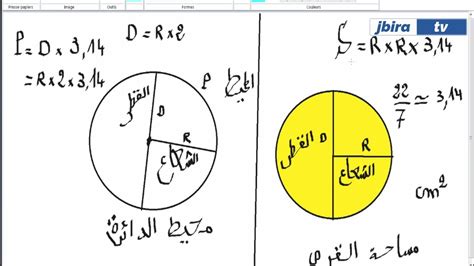
الدائرة هي شكل هندسي مشهور ، أثار انتباه القدماء من المصريين واليونانيين ، حيث كانوا يحاولون إيجاد طريقة لحساب منطقتها

ثم جاء أرخميديس وقام ببعض الجهود والتجارب باستخدام الحاكم والخلفات لتحويل الدائرة إلى مربع في نفس المنطقة ، لكنها فشلت ، وكانت هذه الجهود تسمى عملية التربيع للدائرة.

خصائص ومميزات الدائرة

• لديها وتر تُعرف السلسلة باسم الخط بين كل نقطتين في محيطها.
• وعندما تمر هذه الخيمة إلى المركز يلمسها المكان ، وهو أطول وتر يمكن سحبه لنفس الدائرة
• هناك نسبة مئوية ثابتة بين المحيط والقطر ، وهذه النسبة يرمز إليها شرب ” π هي نسبة موحدة ، مهما كانت مختلفة مساحة الدائرةوقيمته متساوية 3.14 .
• محيط الخط المحيط بالدائرة.
• الظل إنه خط يقصر نقطة واحدة فقط على محيط الدائرة.
• لديها شعاع المسافة بين المركز وكل نقطة في المحيط وترمز للرمز “NA”.

استنتاج قانون مساحة الدائرة

نحن نعلم أن مساحة أي شكل هندسي هي نتيجة ضرب طولها في عرضها ، لكن الدائرة لا تحتوي على أضلاع وبالتالي ليس لها طول أو عرض. مساحة الدائرة وهو:

1. سحبوا دائرة في رسالة.
2. وقاموا بقياس محيطها ونصف قطرها.
3. ثم قطعها إلى 8 أجزاء.
4. ثم يتسلقون أجزاء الدائرة الثمانية بجانب بعضهم البعض ليكونوا شكلًا مستطيلًا.
5. ثم قاموا بقياس الطول وعرضوا هذا المستطيل واكتشفوا ذلك طول المستطيل يساوي نصف محيط الدائرة أو عرض المستطيل هو نصف القطر .
6. ثم ضربوا الطول والعرض التقديمي لإكمال قانون المنطقة مثل هذا:

نصف محيط دائرة الدائرة xx من الدائرة

← ((½) x (π x مع القطر)) x نصف القطر

∴ قانون مساحة دائرة

مثال على حساب مساحة الدائرة

إذا كان لدينا صندوق دائري ، بقطر 6 سم ، ما هي منطقته؟

حل:

1. نجد قيمة نصف القطر بتقسيم القطر على 2 → 6 ÷ 2 = 3
2. بمجرد أن يكون لدينا نصف القطر ، نستخدم القانون لإيجاد مساحة π x نقاء.

← 3.14 × 3² = 28.26 سم مربع

مساحة الدائرة بمعلومية المحيط

يمكننا حساب مساحة الدائرة إذا كنا نعرف محيطها ، مثل هذا قانون محيط الدائرة = 2 x π x na

مثال: إذا عرفنا أن محيط الدائرة يساوي 25.12 سم ، فما هي منطقتها؟

حل:

2 x π x na = 25.12 محيط

2 × 3.14 × Na = 25.12 → نقوم بتعويض قيمة π وقيمة المحيط

6.28 x na = 25.12

Na = 4 سم → الآن بعد أن أصبح لدينا نصف القطر يمكننا العثور على المساحة

π x x² = 3.14 × 4²

= 50.24

مساحة المنطقة في المنطقة تساوي 50.24 سم مربع

وبعد النظر في هذا التفسير والأمثلة التي تم تحليلها ، أصبح العثور على منطقة المقاطعة سهلة بالنسبة لك؟ يسعدنا أن نظهر لنا رأيك.