إن المستطيلات المثالية ، التي تعد واحدة من الشخصيات الهندسية التي تكون قوانينها عديدة ، يمكن أن يشعر الكثير من الناس بسرور كبير عند حل هذه المشكلات الرياضية بسبب قدرتها الكبرى على تحفيز الذاكرة وتحفيز العمليات العقلية والعقلية ، والتركيز وتطبيق القوانين الرياضية. القضايا الرياضية لهذا الشكل الهندسي بالذات.
متوازي المستطيلات
- يتم تعريف المستطيلات المثالية على أنها واحدة من الأشكال الهندسية ثلاثية الأبعاد ، مما يعني أنه يحتوي على الطول والعرض والارتفاع ، وهو على وجه التحديد صورة نمطية مستطيل.
- في بعض الأحيان تكون قاعدة المستطيلات المتوازية مربعة وأحيانًا مستطيلة ، حيث يتم تمييز المستطيلات المتوازية من خلال أن كل وجه متطابق تمامًا في الحجم والمساحة ، حيث أن الطرف المقابل متوازي.
انظر أيضا: يمكن قياس حجم الجسم الصلب من المستطيلات
خواص متوازي المستطيلات
المستطيلات الموازية لها العديد من الميزات التي تميزها عن أشكال أخرى ، فيما يلي أهم عرض تقديمي لهذه الخصائص:
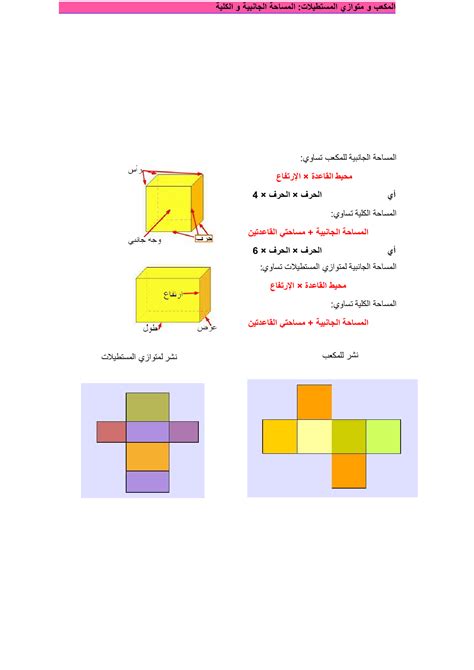
- تتكون المستطيلات الموازية من ستة جوانب ، وهي أربعة جانب ، وجانبين ، أحدهما في الأعلى والآخر في القاع ، ويأخذ كل جانب من هذه الجوانب شكل مستطيل.
- تحتوي المستطيلات الموازية على 12 حرفًا والحرف عبارة عن منطقة اجتماعتين.
- تحتوي المستطيلات المثالية على 8 رؤوس والرأس هي الزاوية التي تملأ ثلاثة أحرف ويحتوي أيضًا على 24 زاوية لأن كل مستطيل يحتوي على أربع زوايا موجودة.
المساحة الجانبية لمتوازي المستطيلات
لتكون معروفة المساحة الجانبية هو سطح لمتوازي المستطيلات باستثناء مساحة الجانبين العلوي والسفلي ويمكن التعبير عنه بموجب القانون التالي: المساحة الجانبية = 2 × ارتفاع مستطيلات متوازية x (طول متوازي + عرض متوازي)
هذا يعني أن المساحة الجانبية = 2 x c (a+b) ، كما (c) يمثل ارتفاع المستطيلات ، كما هو الحال بالنسبة (أ) يمثل طول المستطيلات المتوازية ، (ب) يمثل عرض المستطيلات المتوازية.
هناك قانون آخر ينص على أن المساحة الجانبية = محيط اللائحة x الارتفاع وقانون مربع قاعدة مربعة = طول الضلع × 4 ، ولكن إذا كانت القاعدة مستطيلة ، فإن قانون قرب القاعدة = (طول + عرض) × 2.
مثال توضيحي
- سؤال: ما هذا المساحة الجانبية لمتوازي المستطيلات إذا كان طول قاعدته 8 سم ، فإن عرضه 6 سم ويبلغ ارتفاعه 5 سم؟
- رد: المساحة الجانبية = 2 × مستطيلات متوازية من الارتفاع x (طول + عرض)
المساحة الجانبية = 2 x 5 x (8+6) = 10 × 14 = 140 سم مكعب.
انظر أيضا: القانون المستطيل الأساسي للفضاء
المساحة الكلية لمتوازي المستطيلات
- يتغير إجمالي المساحة لمتوازي المستطيلات في المساحة الجانبية عندما تكون المساحة الإجمالية أكثر من الجانب ، ينص القانون على أن المنطقة الكلية = إجمالي المناطق في المستطيلات الستة.
- تنص صيغة أخرى لقانون المنطقة الكلية على أن المساحة الإجمالية للموازية المستطيلة = المنطقة الجانبية + مجموعة من مساحين أساسيين ، مما يعني أن المساحة الإجمالية = المساحة الجانبية + (المنطقة الأساسية 2) ، والمساحة الأساسية في حالة القاعدة مربعة = طول الأضلاع X ، بينما تكون المساحة الأساسية للقاعدة متساوية.
أمثلة توضيحية عن المساحة الجانبية الإجمالية لمتوازي المستطيلات
لضمان تطبيق المعادلات الرياضية بشكل صحيح ، يجب أن تظهر بعض الأمثلة التوضيحية ، على النحو التالي ،:
| المثال الأول |
|
| المثال الثاني |
|
محيط القاعدة لمتوازي المستطيلات
من خلال إكمال خطابنا المساحة الجانبية لمتوازي المستطيلات المستطيلات الموازية هي واحدة من الأشكال الثلاثة الأبعاد ، وهي محيط أي شكل يمكن اعتباره خيطًا ملفوفًا حول الشكل ، أيًا كان ، أو مستطيلات مكعب ، مثلثات أو أوجه أوجه أماه.
والعديد من الأشكال الأخرى ، لذلك يواجه بعض الأشخاص صعوبات في العثور على محيط قاعدة المستطيل ، ولكن الطريقة الصحيحة للعثور على المنطقة الجانبية وحساب مساحة جميع وجوهها ثم إجراء عملية تجميع لجميع المنتجات المحلية ، ويجدرت الإشارة إلى أن الوحدة المستخدمة هي إما متر مربع أو سنتيمتر.
حجم متوازي المستطيلات
في سياق الحديث عن المساحة الجانبية لمتوازي المستطيلات يشير حجم المستطيلات المتوازية إلى كمية الفراغ في هذا النموذج الثلاثة الأبعاد ، لذلك من الممكن بسهولة التعرف على حجم المستطيلات المتوازية من خلال تطبيق القانون بسهولة: حجم المستطيلات الموازية = الطول x الارتفاع x.
أمثلة توضيحية
يجب توضيح بعض الأمثلة لضمان تنفيذ قوانين الرياضة بشكل صحيح ، لذلك سنقوم بحل بعض الأمثلة من خلال الجدول التالي:
| المثال الأول |
|
| المثال الثاني |
|






اترك تعليقاً